Diabetes Mellitus (DM) is a metabolic disorder characterized by chronic hyperglycemia. The International Diabetes Federation (IDF) suggests that the number of adults living with diabetes worldwide will further expand by 50.7% by 2030. Evidence shows that DM is claiming the lives of more than 4 million people worldwide annually and developing countries account for a substantially high proportion. Similar to other developing countries little is done to quantify the prevalence of chronic diseases and their risk factors in Ethiopia. The general objective of this study has been to model survival of diabetic patients who were under follow-up at Nekemte referral Hospital. This study incorporates secondary data. Of 1953 target population patient 354 are used and randomly selected from the study area. On parametric and semi parametric survival model are used in this study. In this study, a sample of 354 diabetic patients was considered. The medical cards of those patients were reviewed, out of which 160 were female and 194 were male. Among those patients 13.3% and 86.7% were died and censored respectively. The result of the study reveals that a sample of 354 diabetic patients was considered and of those patients was reviewed, out of which 160 were female and 194 were male. Among those patients 13.3% and 86.7% were died and censored respectively. The result of multivariable cox regression model reveals that Survival of diabetic patients was significantly related with body mass index, alcohol use, tobacco use, type of diabetic disease diagnosed, blood pressure, and family history of diabetes mellitus. Therefore, it conclude that Patients involved in risky behaviors such as taking alcohol, smoking cigarette, overweight, high blood pressure, and positive family history of diabetics, have higher death rate. The cox proportional model is fit the data well. This study recommend that the government and concerned bodies should work on perception about the disease and its significant risk factors, so that patients should be well informed about the disease, early diagnose and to follow up their diabetes mellitus status to minimize the significant risk of death.

Introduction

Back ground of the study

Developing countries are encountering a growing burden of chronic diseases, besides infectious diseases and nutritional problems. Although chronic diseases represent a considerable proportion of the disease burden in the African (WHO, 2002), adequate efforts are not devoted to their prevention and control (WHO and ARHO, 2005). According to the world health organization’s statistics, chronic diseases such as CVDs, diabetes, cancers, obesity and respiratory diseases account for about 60 percent of 56.5 million deaths each year and almost half of the global burden of diseases [1].

Diabetes Mellitus (DM) is a metabolic disorder characterized by chronic hyperglycemia. The global burden of diabetes has increased twelve fold between 1985 and 2011 [2]. The International Diabetes Federation (IDF) suggests that the number of adults living with diabetes worldwide will further expand by 50.7% by 2030. Evidence shows that DM is claiming the lives of more than 4 million people worldwide annually and developing countries account for a substantially high proportion.

Diabetes was considered as one of the main global health issues in the world and the trend of diabetic sufferer was currently showing a significant increase. According to Health department, the estimated number of people with diabetes will increase from 151 million people in 2000 to about 221 million people in 2010. An increase of 70 million people was equivalent to an increase of 46% within 10 years of time frame. Prediction compiled by Dr. Hillary King of the World Health Organization indicated that this figure will rise to 300 million by the year 2025 [3]. Recent estimate indicate that 5 to 8 percent of urban adult population in Dares Salaam and in South African townships are affected with diabetes, while 20 to 33 percent have hypertension. In addition, these conditions tend to affect economically active adults, on whom young and old members of the population are often dependent [4].

Similar to other developing countries little is done to quantify the prevalence of chronic diseases and their risk factors in Ethiopia. Small-scale surveys of bank employers in Addis Ababa and Ethiopian medical patients at different times have revealed the existence of these diseases and their risk factors besides an increasing trend of myocardial infarction admission was also recorded from 1988 to 1997 [5]. A burden of disease analysis carried out in rural Ethiopia found that chronic diseases have contributed to 24% of DALYs lost compared to 72% for other health problems including communicable diseases. According to the ministry of health report of health and health related indicators, hypertension without mention of heart was the ninth cause of death nationwide in 2003/04 (MOH, 2003/2004).

According to WHO estimate, the number of diabetic cases in Ethiopia in 2000 were 800,000 and is expected to increase to 1.8 million by 2030 [6]. Thus, this study has been designed to modeling the survival time and identifies predictive risk factors associated with survival of patients with diabetes mellitus at Nekemte Referral Hospital. The general objective of this study has been to model survival of diabetic patients who were under follow-up at Nekemte referral Hospital. IDFA reported Ethiopia to be ranked 3rd among the ten top countries in Africa with 1.4 million DM cases and estimated prevalence of 3.32% by year 2012.

Data and Methodology

Study area and source of data

The study conducted in East Wollega zone Nekemte town in Nekemte hospital, Oromiya Ethiopia. The town is located at 328 km to the west of Addis Ababa in Oromiya region. The town has an attitude and longitude of 9° 5N, 36° 33E respectively and elevation of 2088 m3. And also it has a temperature range from 14°C -26°C and annual rainfall estimated to 1500-2000 m3. This study incorporate secondary data. The hospital’s registry was used to retrieve data on diabetes mellitus and patients initial date of entry to follow-up. In the study, all diabetic patients who were recorded in the medical record room of the Nekemte Hospital and those cards which have the vital data for the research were included in the study. All patients whose age was recorded in their treatment card were included in the study without any restriction on the age of the patients.

Sampling design and sample size determination

This study is based on retrospective study (i.e. all the events - exposure had already occurred in the past), which reviews the patient cards and patient’s information sheet and investigate the risk factors associated with the survival of patients with DM diseases. The source of the data was from the patients that were registered at the Nekemte Hospital with the case of DM. The sample selection mechanism that used was simple random sampling method in which each of the patients had equal chance of being selected to be part of the study.

In conducting researches that require taking a sample, we always have the stage of deciding the sample size. The decision is important because taking too large sample implies waste of resources while too small sample reduces the usefulness of the results. In order to have an optimum sample size, there are a number of issues/points one has to take into account. Some of the issues are: objective of the research, design of the research, cost constraint, degree of precision required for generalization and etc.

Based on the above information, there are several formulas developed for sample size calculation that conform to different research situations. Accordingly, the sample size determination formula is adopted for this study [7].

n = ((z2 p (1-p))/d2)/ (1+1/N [(z2 p (1-p))/d2 -1])………1

Where, n = the sample size needed, N = the total population size, Z is the upper α⁄2 points of standard normal distribution with α = 0.05 significance level.

Suppose the maximum allowable difference between the maximum likelihood estimate and the unknown population parameter denoted by d, desired to be 0.024 .The specification of d must be small to have a good precision. The parameter represents proportion of death due to DM disease. A few previous studies describe the proportion of death due to DM disease in Ethiopia. In this study, the estimated proportion of death due to DM disease to be 0.07 [8]. Hence, the sample size with, N = 1913, together with above specifications was, n = 354. The response or outcome variable is the length of time until the event of interest takes place (death) or until some point in time where the patient is no longer followed (e.g., a patient is lost to follow-up or is still alive at the end the study i.e. censor ). When the latter occurs, the patient survival time is said to be censored. Also, 9 potential explanatory variables were considered in this study (Table 1). Detailed description of all variables related to diabetes patient is presented as follows

Methods of Data Analysis

Survival analysis

Generally, biometric system involves two basic biometric processing modes namely, the enrolment and verification modes. The two basic modes involve sub stages for its processes as depicted in figure 1.

Figure 1:

It is widely used in areas that deal with biological organism and failure of mechanical systems. It is a branch of statistical analysis that are commonly seen in engineering, economics or sociology when modeling time to event data, such as death of diabetes mellitus patient, failure of a equipment. The difference of survival analysis is that it deals with censoring. Censoring is a form of missing data problem which is common seen in those above mentioned areas. A survival function measures the probability of non-event after certain time which defined as

S(t) = Pr (T > t)………2

Where “t” some time and T is a random variable denoting the time of an event. According to definition, a survival function is always between 0 and 1. It must be non-increasing and approaches 0 as time goes to infinitely.

Kaplan - meier estimator

Nonparametric analysis is used to analyze data without assuming an underlying distribution which avoids potentially larges errors brought about by making incorrect assumptions about the underlying distribution. A plot of Kaplan - Meier estimate of the survival function is a series steps of declining magnitude. When the sample size is large enough with respect to the population, Kaplan-Meier estimator approaches the true survival function for the population.

Let S (t) is the probability that an individual will not have re occurrence of an event after time t. For a sample of size n, denote the observed times until death of n sample members as $$t_1\le t_2\le \mathrm{..........}\le t_n$$ . Then the nonparametric Kaplan-Meier estimator of the survival function is estimated by:

$$\widehat{S}(t)={\displaystyle \prod _{t_i\le t}\frac{n_i-d_i}{n_i}}$$

Where n$$n_i$$ the number of individual who are alive is just before time t_i and d_i is the number who died during this time.

In general, if the plot shows the pattern of one survivorship function lying above another, this means the group defined by the upper curve lived longer, or had a more favorable survival experience than the group defined by the lower curve. But, the statistical question is whether the observed difference seen on the plot is significant. This needs to be answered using appropriate statistical test [9]. The general form of test statistic that deal with this issue is given as

$$Q={\frac{\left[{\displaystyle \sum _{}^{}{w}_i(d_{1i}-{\widehat{e}}_{1i})}\right]}{{\displaystyle \sum _{i=1}^m{w}_i^2{\widehat{v}}_{1i}}}}^2{\widehat{e}}_{1i}=\frac{n_{1i}{d}_i}{n_i}\text{and}{\widehat{v}}_{1i}=\frac{n_{0i}{n}_{1i}{d}_i(n_i-d_i)}{n_i^2(n_i-1)},\mathrm{..........................}[3]$$

Where m is the number of rank-ordered failure (death) times.

n_0i is the number of individuals at risk at observed survival time t(i) in group 0

n_li is the number of individuals at risk at observed survival time t(i) in group 1

d_0i is the number of observed deaths in group 0

d_li is the number of observed deaths in group 1

n_i is the total number of individuals or risk prior to time $$t_{(i)}$$

d_i is the total number of deaths at time $$t_{(i)}$$

W_i is the weight for censor adjustment at failure time $$t_{(i)}$$

Regression models for survival data

Cox proportional hazard model: An alternative approach to modeling survival data is to Cox Proportional Hazard (Cox - PH) model which assumes that the effect of the covariates is to increase or decrease the hazard function by a proportionate amount at all durations. Thus,

$$\lambda (t,x)={\lambda }_0(t)e^{x\beta }\text{or}\ln \frac{\lambda (t,x)}{{\lambda }_0(t)}=x^{\prime }\beta \mathrm{..............................}[4]$$

Where $${\lambda }_0(t)$$ is the baseline hazard function or the hazard for an individual with covariate values 0, and $$e^{x^{\prime }\beta }$$ is the relative risk associated with the covariate values x. Subsequently, for the survival functions

$$S(t,x)=S_0{(t)}^{e^{\prime }\beta }\mathrm{.........................................................}[5]$$

Hence the survival function for covariates x is the baseline survivor raised to a power. Parameter estimates in the Cox-PH model are obtained by maximizing the partial likelihood as opposed to the likelihood. The partial likelihood is given by

$$L(\beta )={\displaystyle \prod _{Y_{i}uncensord}\frac{\exp (x^{\prime }\beta )}{{\displaystyle {\sum }_{Y_j\ge Y_j}\exp (x_j^{}\beta )}}}\mathrm{...................................}[6]$$

The log partial likelihood is given by

$$l(\beta )=\log L(\beta )={\displaystyle \sum _{Y_{i}uncensord}\{x_j^{}\beta -\log [{\displaystyle \sum _{Y_j\ge Y_i}\exp (x_j^{}\beta )}]\}}\mathrm{..................}[7]$$

Result and Discussion

Descriptive Statistics

In this study, a sample of 354 diabetic patients was considered. The medical cards of those patients were reviewed, out of which 160 were female and 194 were male. Among those patients 13.3% and 86.7% were died and censored respectively. A death proportion of females which is 11.9% seem lower than males 14.4 %. There are 12.71% and 87.7% patients from rural and urban areas, the death proportion of rural residents were 28.9% higher than urban residents 11%, respectively. Regarding to body mass index, which measure a body fat based on height and weight showed that 42(11.86%) were under weight, 126(35.59%) were healthy and the rest 186(52.25%) were overweight. The death proportion of overweight, normal and underweight patients were 11.9%, 2.4% and 20.96%, respectively.

Out of the entire subjects integrated in this study, 73(20.62%) of the patients were alcohol users whereas 251(70.9%) were nonalcoholic. The death proportion was higher for those alcohol users 23.3%, while lower for those nonalcoholic patients 10.7%. The sample data also revealed that 229(64.68%) patients were nonsmokers and 125(35.31%) were smokers. The death proportion of smokers 23.2% was higher than non-smokers 7.9%.

The outcome in table 2 also revealed that, 173(48.87%) patients were diagnosed with type 1 DM and 181(51.12%) patients were diagnosed with type 2 DM. T ype-1 diabetics were more likely to dead (22.5%) compared to type-2 diabetics (4.4%). From all patients included in this study, the highest proportion 177(50%) of the patients had normal blood pressure, followed by those who had high blood pressure 106(29.94%), while the lowest proportion 71 (20% ) of the patients had uncontrollable blood pressure at first diagnose. The death proportion of patients who had uncontrollable blood pressure were 46.5%, followed by those who had elevated blood pressure which was 10.4%, while the lowest proportion of death 1.7% were accounted for patients who had normal blood pressure. Out of the total sample, 144(40.67%) patients had no pre-existing health problem, 115(32.48%) had hypertension and 95(26.84%) had dyslipidemia. Regarding pre-existing health condition, the death proportion were higher which is 34.7% for those patients who had bad dyslipidemia, followed by those who had hypertension 9.6%, while smaller 2.1% for those who had no pre-existing health problem. The proportions of patients who had negative family history of diabetes mellitus were 238(67.23%), whereas 116(32.3%) had positive family history of diabetes mellitus. The death proportion were higher for those patients who had positive family history of diabetics 15.1%, while smaller for negative family history of diabetics 9.1% [10].

Comparison of survival experience

In comparison of survival experience using Kaplan-Meier estimates if the plot shows the pattern of one survivorship function lying above another, this means the group defined by the upper curve lived longer, or had a more favorable survival experience than the group defined by the lower curve. In order to investigate if there is significant difference between the survivals of a patient by gender, Kaplan-Meier survivor estimates for the two gender groups are plotted and the Figure shows that females had slightly higher survival until the 4 year compared with females whereas; both survive the slightly the same after 4 years. But the difference in survival was not supported by Statistical tests, since log-rank (mantel cox) test. The long rank test shows that there is insignificant difference between male and female with respect to survival time.

Comparing the survivor functions between different categories BMI of diabetic patients, Kaplan Meier survivor estimates for the three body mass groups are plotted and the figure shows that patients with normal body weight had slightly higher survival compared with underweight and overweight patients. Statistical test is made by using log-rank (mantel-cox) test shows that there is significant difference between patients whose body mass index was normal, underweight and overweight with respect to survival time. Among different diabetic categories, type 1 DM patients had the lowest survival time and it is also statistically significant (p =.000). As the results depicts that patients with poor health indicators like drinking alcohol, smoking tobacco, high blood pressure, pre-existing health problem and positive family history of DM had small survival time and all are highly significant(p < .000). The information presented above is summarized in the following table 3.

Univariate analysis

Univariate analysis is an appropriate procedure that is used to screen out potentially important variables before directly included in the multivariate model. In any data analysis it is always advisable to do first univariate analysis before proceeding to more complicated models. The relationship between each covariates and survival time of diabetic patients are presented in table 4 As can be seen from this table, survival of the patients is significantly related with age, alcohol use, tobacco use, body mass index, type of diabetic disease diagnosed, blood pressure, pre-existing health condition, and family history of diabetes mellitus. But the covariates genders are not statistically significant at 0.25 of significant level. Furthermore, using a modest level of significance 25% to include in the multiple covariates model for further investigation are Gender, age, alcohol use, smoking , body mass index, type of diabetic disease diagnosed, blood pressure, pre-existing health condition, and family history of diabetes mellitus.

Survival of diabetic patients was significantly related with body mass index, alcohol use, tobacco use, type of diabetic disease diagnosed, blood pressure, and family history of diabetes mellitus. The values of the Wald statistic for individual 𝛽 coefficients support that the estimated values 𝛽i’S are significantly different from zero at 𝛼 = 5% level of significance for all the above covariates. The remaining variables which were used in the single covariate analysis (such as age, place of residence and region ) are found to be non-significant.

Assessment of model adequacy

The formal test to check the cox proportional assumption model in the following table 5 shows the time-dependent covariates (interaction of covariates with time) were not significant for body mass index, alcohol use, tobacco use, blood pressure, Type of diabetes and family history of DM which justifies the proportional hazard assumption holds at 5% level of significance.

Figure 2: Cumulative hazard plot of the Cox-Snell residuals of the proportional hazards Cox regression model

Identification of influential and poorly fitted subjects

Outliers in Cox proportional hazard model can be divided into three categories. There are: Subjects that have value of a covariate that differs from the sample average to a great extent (1), subjects that have strong influence on parameters estimates (2) subjects that have strong influence on the partial likelihood function value and thus on the model adequacy. Like linear regression diagnostics, the influence of each observation can be accessed through ∆β and overall impact measures like Cook’s distance. That is, the model is estimated with the entire dataset, and then the effect of the i^th observation on the estimates is assessed by fitting the model without the ith observation and comparing to the original results. If the differences are substantial, there is concern about influence. Delta-Beta: For parameter βj, the impact of observation ‘i’ on the estimate is assessed with: ∆β _j(i) = β_i - β _j(i)

The smallest and highest differences of the parameter estimates of the variables included in the final model when the data value for each child is deleted from the mode.

From the above output of DEFBETA no observation regarded as influential observation because for any case, if |DFBETA| > 1 for small data sets or $$\text{2}/\sqrt{\text{n}}$$ for large data sets, then that case can be regarded as influential. So in the above table 6 from the highest difference column there is no any observation their |DFBETA| >1 means that the model fits the data.

Therefore, we conclude that there are no influential subjects. Also based on graphical assessment of influential observation from the appendix we conclude that from all of the above graphical assessment of influential observation no variables can have influential poorly fitted.

Checking for overall goodness of fit

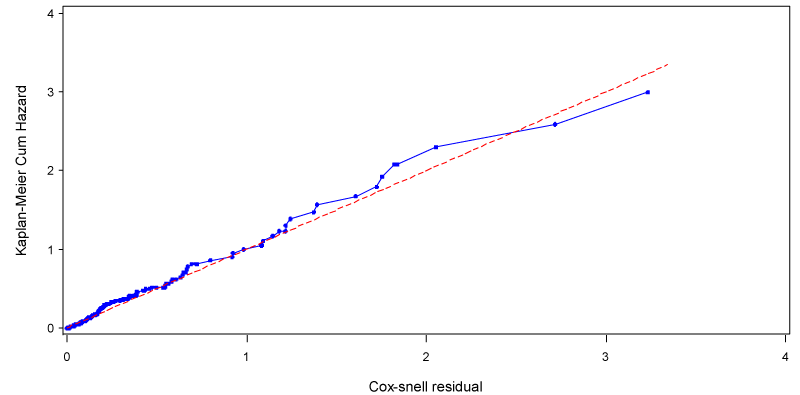
The final step in the model assessment is to measure the overall goodness of fit. For this objective we use the Cox-Snell residuals and R2. The plot of the Nelson-Aalen estimate of the cumulative hazard function of the Cox-Snell residual against the Cox-Snell residuals is presented in Figure below.

The above figure is Cumulative hazard plot of the Cox-Snell residuals of the proportional hazards Cox regression model. The 450-striaght line through the origin is drawn for reference.

It can be seen that the plot of the residuals in the above Figure is fairly close to the 450 straight line through the origin. Thus, the plot is evidence that the model fitted to the data is satisfactory. Moreover, an adequate model may have low R2 due to high percent of censored data. We use R2 as a measure of overall goodness of model fit. As it is defined in chapter three, it is given as:

R²= 1-exp (2/n (LL₀-LL_β‘))

Where n = 354 is the number of observation, LL₀= 497.478 is the log partial likelihood for model without any covariates and LL_β‘ = 428.374 is the log partial likelihood for model with covariates. Then R_p² =1-exp {2/354 (497.478-428.374)} = 0.4775. Thus, the model fitted for the study has the value, which is small, indicating that the model fit the data well.

Interpretation and presentation of the final model

The model that fit to the diabetic patient’s data in table 1 has seven categorical covariates (BMI, alcohol use, tobacco use, BP, and family history of DM). The model adequacies it suggested that the model is in good fit. Thus, the Cox regression coefficients in the final model are interpreted as follows. After adjusting other covariates, the risks of death of patients having abnormal blood pressure, has been increased. The hazard of those patients, having high blood pressure is .605 times the hazard of those having a normal blood pressure (adjusted HR = 0.027, 95%(0.007-0.097)). Similarly, the hazard of those patients who had uncontrollable blood pressure is 1.164 times the hazard of those patients who had normal blood pressure (Adjusted HR = 1.164 , 95%(.533, 2.542)) which means that the survival time of patients who had normal BP is too fold when compared with patients who had uncontrollable BP.

Looking at BMI, after adjusting other covariates, patients who had normal BMI are found to be associated with high survival time, whose hazard rate is .348 times that of underweight patients (adjusted HR= .348 95% CI =.121-2.108). Similarly, the hazard rate of patients who are overweight is 8.285 times that of patients who had been underweight (adjusted HR = 8.285, 95% CI = 2.71-25.25). On the other hand, the hazard rate of patient who use tobacco or smoking is about 2.054 times higher than patients who didn’t use tobacco or smoking (adjusted HR = 2.054, CI = 1.111-3.8000). Looking at the effect of alcohol use after adjusting other confounding variables, the hazard of those patients who took alcohol was 1.935 times the hazard of those who didn’t take alcohol (adjusted HR = 1.935, C = 1.01-3.68) indicating that the survival time is reduced by 93.5%.Similarly the hazard of those patients who have type 2 was 3.257 times the hazard of those who had type 1 diabetes mellitus (adjusted HR = 3.257, CI = 1.495-7.099).

Finally, family history of DM is another predictor variable related with risk of death of patients. The hazard of patients who had family history of DM were found to be 2.075 times the hazard of those who does not have any history of DM (adjusted HR = 2.075; 95% CI = 1.185-3.63) [11].

Conclusions and Recommendation

Conclusion

The objective of the study was to identify significant risk factors that affect survival of diabetic patients who have been under follow-up at Nekemte Referral Hospital. For determining the risk factors for the survival of diabetic patients and modeling the survival time, a total of 354 patients were included in the study out of which 160 were females and 194 were males. Among those patients 13.3% were died and the rest were censored. The Cox regression analysis showed that the major factors that affect the survival of diabetic patients are body mass index, alcohol use, tobacco use, diabetic complications, blood pressure, and pre-existing health conditions and type of diabetes and family history of diabetes mellitus. Patients involved in risky behaviors such as taking alcohol, smoking cigarette, overweight, high blood pressure, and positive family history of diabetics, have higher death rate. The result of this study also indicated that survival probability of a patient is not statistically different among groups classified by sex, age, place of residence, and region.

Recommendations

Based on the result of the study different factors are identified for the death of diabetic Patients. The following recommendations are made:

 The government and concerned bodies should work on perception about the disease and its risk factors, so that patients should be well informed about the disease, early diagnose and to follow up their diabetes mellitus status to minimize the risk of death.

 Future studies also need to assess the level of awareness, treatment and control of these risk factors. The economic and social consequences of diabetes mellitus and other chronic diseases should also receive due attention in future research, as these diseases involve lifelong medical care and social support with significant socioeconomic burden to the individual and the society at large.

Acknowledgments

First of all great thank goes for my almighty God Jesus for all his encouragement and continues help to conduct this research and finalize it to this stage. I gratefully acknowledge the Wollega.

University and Nekemte Hospital for helping me relevant material to undertake the study and data collection.

1. Abdesslam B, Saber, B. The burden of non-communicable diseases in developing countries. Int J Equity Health. 2005; 4: 3-9. DOI: 10.1186/1475-9276-4-2
2. Abreham Berhane. Statistical modeling for the recurrence of cervical cancer: A case study at tikur anbessa referral hospital, Addis Ababa, Ethiopia. Master thesis Hawassa University, department of statistics, Hawassa, Ethiopia. 2011.
3. Incidence of type 1 diabetes. American Diabetes Association. 2007. https://bit.ly/39zpIF8  
4. Barcelo A, Rajpathak S. Incidence and prevalence of diabetes mellitus in the Americas. Rev Panam Salud Publica. 2006; 10: 300-308. DOI: 10.1590/s1020-49892001001100002
5. Agresti A. An introduction to categorical data analysis. Wiley and Sons. 1996. https://bit.ly/3f0wVPC
6. Allison PD, Liker JK. Analyzing sequential categorical data on dyadic interaction. Psychological Bulletin.1982; 91: 393-403. https://bit.ly/333x56x
7. AmosAF, Carty DJ, Zimmet. The rising global burden of diabetes and its complications. Estimates and projections to the year.1997; 2010. https://bit.ly/30040qA
8. Alvin C. Diabetes mellitus, harrison‟s principles of internal medicine, 17th Ed. 2008; 22: 75-304.
9. Allison PD. Event history analysis: Regression for longitudinal event data. Beverly Hills, CA: Sage. 1984. DOI: https://dx.doi.org/10.4135/9781412984195
10. Beran D, Yudkin JS. Diabetes care in sub-Saharan Africa. Lancet. 2006; 368: 1689-1695. https://bit.ly/2WWTjD8
11. Bjork S. Global policy aspects of diabetes in India. Health Policy. 2003; 66: 61-72. DOI: 10.1016/s0168-8510(03)00044-7