Aim: In modern radiotherapy high energy photon beams are produced by linear accelerators, fast and accurate calculation of the dose distribution in patient’s body is required. Computer systems known as treatment planning systems (TPS) calculate the dose distribution. Medical Physicists use the treatment planning systems for radiotherapy dose calculations. Every TPS should be checked for the accuracy of the computed dose compared to dose measured with ion champers under several cases, before it can be used clinically. Modern techniques like intensity modulated radiotherapy (IMRT) require dose calculation accuracy. The aim of this study is to create dose calculation software in order to verify the accuracy of the TPS.

Material and method: We created an independent routine in MATLAB that calculates absorbed dose at any point on the central axis of a photon beam in water and we used it to check the accuracy of the treatment planning calculation. In this study we compared the Siemens Once 6 MV linear accelerator dose measurements to Nucleation Master plan TPS calculations.

Results and conclusions: The results showed agreement between dose measurement and dose calculation better than 3 percent at any case. The advantage of the MATLAB software is that it can calculate the dose at any point on the beam’s central axis very fast and it gives the medical physicist the opportunity to check the TPS calculation for several depths in the water and for several field sizes in a very short time period.

Introduction

At every new linear accelerator installation, dose characteristics must be measured thoroughly [1]. Absorbed dose to water is measured with ion champers and electrometers. Dose metrics are presented as Percentage Depth Doses (PDD), dose profiles at the two main horizontal axes of the linear accelerator (in plane and cross plane) [2]. Also collimator scatter factors (Sc), phantom scatter factors (Sp), output factors (Scp) are obtained from ion champers measurements [3]. From these dosimetric quantities it is possible to calculate the Monitor Units (MU) needed to irradiate a point at a mass of water to a certain amount of absorbed dose [4]. Monitor unit is the definition of the radiation output of the linear accelerator. One monitor unit defines one cGy of absorbed dose in water at reference conditions. Reference conditions usually are 10 x 10 cm² field size at the depth of maximum dose and Source to Skin Distance (SSD) 100 cm. Several commercial computer systems known as Treatment Planning Systems (TPS) calculate the dose distribution in the human body when it is irradiated with a linear accelerator. The dose characteristics that were measured for the linear accelerator are inputted in the TPS and the program calculates the MU’s that are needed for complex fields, field sizes and dose distributions in the human body [5]. It is very important for the safety of the patient and the quality of the treatment to check the accuracy of the TPS calculations under every possible situation [6]. The accuracy of the TPS calculations can be checked by comparing the TPS calculation against the ion chamber dose measurement. Independent software was created in MATLAB that calculates dose at any point in the central axis of a photon beam in water and it was used to check the accuracy of the treatment planning calculation. The advantage of the MATLAB software is that it can calculate the dose at any point on the beam’s central axis very fast and it gives the medical physicist the opportunity to check the TPS calculation for several depths in the water and for several field sizes in a very short time period.

Materials and Methods

The linear accelerator

A Siemens linear accelerator model Oncor Impression is installed at Aretaieion Hospital in Athens since 2006. It can produce 6 MV photon beam and it has Multi Leaf Collimator (MLC). Complex field shapes can be generated with the MLC leaves that have one centimeter width at the isocenter. The linear accelerator can also deliver step and shoot Intensity Modulated Radiotherapy (IMRT) beams [7]. Static radiotherapy beams deliver practically constant intensity at every point of the beam field. The IMRT beams can deliver different intensity at the points of the beam field. The advantage of this technique is that the part of the beam that passes through the target can have high intensity and the part of the beam that pass through the healthy tissue can have lower intensity. Dosimetric characteristics of the linear accelerator were measured with commercial water phantom, ion champers and electrometers. The dosimetric characteristics, PDD’s, profiles and output factors were inputted into a commercial TPS, the Elekta oncentra Master plan version 4.3. The PDD is defined by the equation PDD = 100*D_p/D_o were D_p is the dose at a point at depth p and D_o is the dose at the reference point. The reference point is located at the depth of the maximum dose. The beam profile is the dose distribution along the main axis of the beam field. It is measured at several depths in water for the two main axis of the beam field. The output factor is defined by the equation OF = D(a,d_r)/D(a_r,d_r) were OF is the output factor, D(a,d_r) is the dose of the field size a at the reference depth and D(a_r,dr_r is the dose of the reference field size at the reference depth. Usually the reference field size is 10 cm x 10 cm and the reference depth is 10 cm of water. The TPS uses a collapse cone algorithm and can reproduce the linear accelerator dosimetric characteristics [8]. Photons interact with tissue and deposit energy at and around the interaction point. Dose is calculated by the convolution of the total energy released at the material with the point kernel. The point kernel is pre calculated dose distribution around the point of interaction. The collapse cone algorithm uses cone kernels that the energy deposited inside the cone is collapsed into the central axis of the cone.

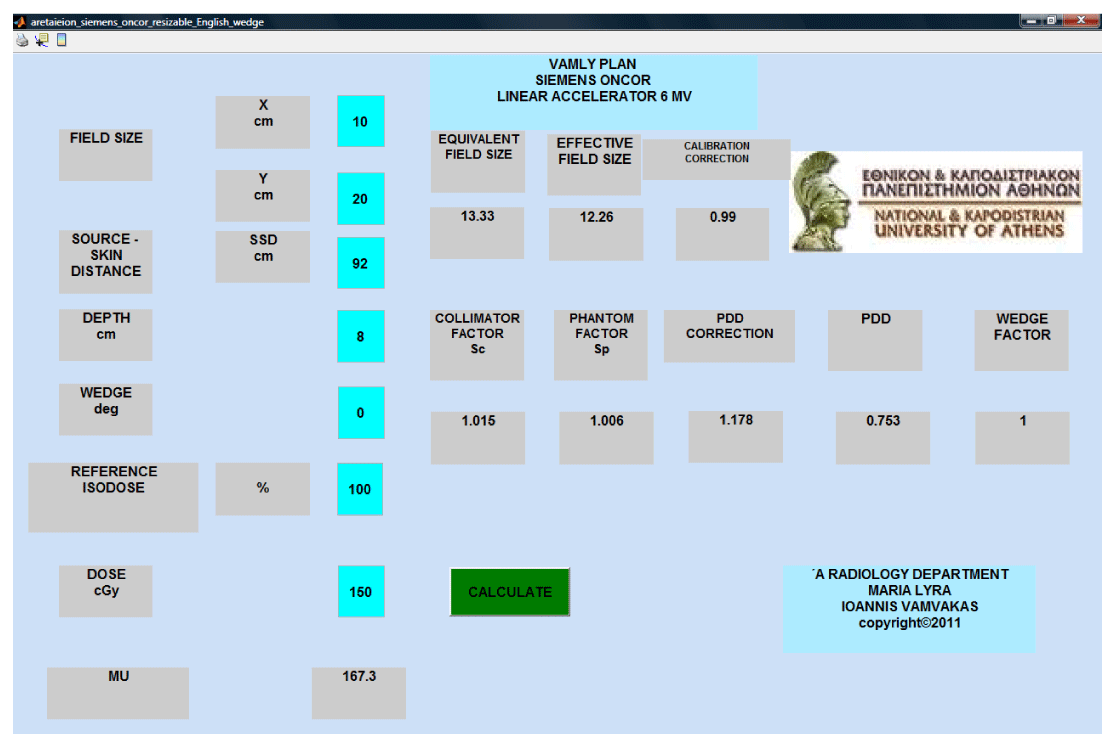
The accuracy of the reproduction was checked before the system was clinically commissioned. In order to check the MU accuracy, special software was created in MATLAB. The software was named VAMLY plan(VAM comes from Vamvakas and LY from Lyra, the surnames of the main and the senior researchers) and it can calculate the MU’s that are needed to deliver a selected absorbed dose to water at any point on the central axis of the beam.

The Vamly Plan

The VAMLY plan is a stand-alone computer application written with the MATLAB code. Once the dosimetric characteristics of the linear accelerator are inputted in the application, the user can calculate the MU’s needed for a specific dose on the beam’s central axis. PDD’s, Sc’s, Sp’s and wedge factors for rectangular field sizes from 4x4 until 40x40 cm² are inputted in the VAMLY plan. The MU calculation is performed according to the Khan methodology. In case that a calculation requires data values between the original inputted data, linear interpolation is automatically performed. At the graphical user inter phase, the user types the beam dimensions at the isocenter for the in plane (X) and the cross plane (Y) direction. Next, user has to type the SSD, the depth, the wedge angle (zero value at the wedge is valid for open fields), the reference isodose and the absorbed dose. Next the user has to click on the ‘CALCULATE’ button and the program displays the calculated MU’s. Also the equivalent and the effective field sizes, the calibration correction, Sc, Sp, PDD and wedge factor values are displayed for every calculation.

The algorithm

The algorithm was written in the MATLAB code. The first two inputs that define the beam dimensions at the isocenter must be numbers. The program prompts the user to insert a number between 0.5 cm and 40 cm that is the maximum possible field size. If the input is invalid then an error dialog box informs the user that the input is invalid. The third input is the SSD. The SSD input must be a number between 40 cm and 400 cm and defines the distance between the radiation source and the patient’s skin. The program prompts the user to type a valid insert and an error dialog box open if the input is invalid. The forth input is the calculation depth. The input must be a number from 0.5 cm to 30 cm. The program also prompts user for a valid input and error dialog box appears if the input is invalid. The fifth input is the wedge angle. The program prompts the user to insert zero (0) for open field or 15, 30, 45, or 60 for a physical wedge of 15, 30, 45, 60 degrees respectively. Error dialog box is opened if the input is invalid. The sixth input is the reference isodose. The default input is 100. The last input is the delivered dose. The algorithm calculates the equivalent square field size and the effective field size using the first three inputs according to the Khan methodology. This part of the code is shown below.

Total = 2* str2num (a)* str2num (b)/ (str2num (a) + str2num (b));

Total = round (total*100)/100;

c = num2str (total);

total2 = str2num (d)* str2num(c)/100;

total2a = round (total2*100)/100;

e = num2str (total2a);

Where a is x dimension, b is y dimension and d is the SSD.

Then the algorithm calculates the factor for SSD different than 100 cm and the factor for dose calibration point different than 1.5 cm depth and SSD 100 cm using the code below.

Total 3 = 101.5 ^ 2 / (str2num (d) + 1.5) ^2;

Total 41 = (str2num (d) + 1.5) ^ 2 / (str2num (d) + str2num (f)) ^ 2;

Total 42 = (100 + 1.5) ^ 2 / (100 + str2num (f)) ^ 2;

Where ‘f’ is the depth of the calculation point.

The measured Sc and Sp values for several field sizes are loaded into the program. These data are loaded as two separated tables. One table is for Sc and another for Sp. The first row is the Sc (or Sp) values and the second row is the field size respectively. The algorithm calculates the Sc value using the Sc table and the equivalent field size with the command interp1 from MATLAB. This command executes linear interpolation between the two closest measured Sc values for the calculated equivalent field size. With the same way the Sp value is calculated from the Sp table and the effective field size. For the wedged field sizes, a wedge factor is assigned to every physical wedge (15, 30, 45, 60 degrees) and the algorithm uses the appropriate wedge factor for the dose calculation. The measured PDD’s for several field sizes are inputted into the program as table. The first row is the square field size. The column below every field size is the PDD for several depths. The last column is the depth. The algorithm calculates the PDD using the inter p2 command [9]. This command makes linear interpolation for the PDD between the closest values of the measured field sizes and depths. The last step of the algorithm is the MU calculation. It is done by dividing the desired dose with all the correction factors that were described above.

Results

MU calculations were performed with the Master plan TPS and with the VAMLY plan and the results were compared. Rectangular fields with dimensions 5x5, 7x7, 10x10, 12x12, 15x15, 18x18, 20x20, 25x25, 30x30, 40x40 cm were selected for the comparison. Calculations were performed for these fields for SSD 100 cm and also for SSD 90 cm for 5 cm and for 10 cm depth. The selected absorbed dose was 200 cGy. Also rectangular 30 degrees wedged fields with dimensions 7x7, 10x10, 12x12, 15x15, 18x18, 20x20 cm were selected to compare the TPS performance for wedged fields at SSD 100 cm, 5 cm depth and 200 cGy absorbed dose. The results showed that the differences between TPS and VAMLY plan were 2.5 % or less for all the selected cases. The statistical analysis showed that the mean difference among the 47 cases was 0.8% and the standard deviation was 1.4.

Figure 1: The VAMLY plan graphical user interphase. At this example user inputed for field size (10 cm x 20 cm), SSD (92cm), depth (8 cm), wedge filter (0 for open field), reference isodose (100%) and dose (150 cGy). Then user pressed the green “CACLULATE” button and the MU’s were displayed (167.3). Also all the required parameters for the specific calculation were displayed (Sc, Sp, PDD, wedge factor and correction factors for calibration and SSD).

Discussion

Cancer is among the leading causes of morbidity and mortality worldwide. Approximately 14 million new cases and 8.2 million cancer related deaths were reported in 2012. It is expected that annual cancer cases will rise from 14 million in 2012 to 22 within the next two decades [10]. Surgery, radiotherapy and chemotherapy are the three basic treatments for cancer [11]. The need for new radiotherapy linear accelerators installations will rise in next decades. Fast and accurate dose calculation is very important in modern radiotherapy. Complex treatments like intensity modulated or volumetric radiotherapy require calculation for a large number of beams [12,13]. The efficiency and safety of the treatment cannot be achieved without accurate dose calculation. TPS’s are essential at every radiotherapy department because they satisfy the demand for fast and accurate dose calculation. The accuracy of the calculation must be checked thoroughly before a new installed TPS is commissioned for clinical use [14]. TPS dose calculation must be compared to hand calculation for several fields and depths. The agreement between TPS against hand calculation should be better than 3 % [15]. Hand MU calculation is time consuming and is not the ideal method for the medical physicist. The VAMLY plan can perform these calculations very fast and easy and it is very helpful to the medical physicist. Time required for a single beam calculation is less than a second and a few seconds are enough for a beam geometry input. At this study we checked the Oncentra Master plan TPS for the accuracy of dose calculation. Agreement between TPS and VAMLY calculation was better than 2.5 % for every tested beam. Time consumed for all the calculations with the VAMLY plan was less than thirty minutes. The estimated time for the above hand calculations is four hours. We assume that five minutes is the time needed to make and recheck a hand MU calculation. In this study forty seven calculations were processed which leads to 3.92 hours needed. It is obvious that the VAMLY plan helps the medical physicist to finish the TPS commissioning at a very shorter time period. Also The VAMLY plan can be commissioned for clinical use in the radiotherapy department for two dimensional radiotherapy treatments. Two dimensional radiotherapy treatments are about 30 % of the total number of treatments in a modern radiotherapy department [16]. The VAMLY plan can very easily perform a large number of clinical dose calculations fast and accurately.

Conclusions

The VAMLY plan can calculate the dose to water delivered at a point on the central axis using PDD, Sc, Sp and wedge factors. The calculation is fast and helps medical physicists to reduce the time needed for TPS commissioning. Also it can perform a large amount of the clinical workload in a radiotherapy department. The VAMLY plan can be used for the clinical commissioning of every other commercial TPS. In the future the VAMLY plan can be developed to perform calculations for complex field shapes like fields blocked with multi leaf collimator. Also it can be developed to provide dose calculations in heterogeneous materials with known density. Finally it can be developed to perform off axis dose calculations if the dose profiles at several depths are inputted in the initial data.

1. Klein EE, Hanley J, Bayouth J, Yin FF, Simon W, Dresser S, et al. Task Group 142 report: Quality assurance of medical accelerators. Med Phys. 2009; 36: 4197-4212. https://goo.gl/YxWgNx
2.  Cho SH, Vassiliev ON, Lee S, Liu H, Ibbott GS, Mohan R. Reference photon dosimetry data and reference phase space data for the 6 MV photon beam from Varian Clinac 2100 series linear accelerators. Med. Phys. 2005; 32: 137-145. https://goo.gl/2aNwvh
3. Indra JD, Chee-Wai C, Ronald JW, Ahnesjo A, Gibbons J, Li XA, et al. Accelerator beam data commissioning equipment and procedures: Report of the TG-106 of the Therapy Physics Committee of the AAPM. Med. Phys. 2008; 35: 4187-4215. https://goo.gl/znenzt
4. Dietmar G. Monitor unit calculation on the beam axis of open and wedged asymmetric high-energy photon beams. Phys. Med. Biol. 1999; 44: 2987-3007. https://goo.gl/CwCVpm
5. Knoos T, Wieslander E, Cozzi L, Brink C, Fogliata A, Albers D, et al. Comparison of dose calculation algorithms for treatment planning in external photon beam therapy for clinical situations. Phys. Med. Biol. 2006; 51: 5785-5807. https://goo.gl/kEJom2
6. Chan J, Russell D, Peters VG, and Farrell TJ. Comparison of monitor unit calculations performed with a 3D computerized planning system and independent ‘‘hand’’ calculations: Results of three years clinical experience. J Appl Clin Med Phys. 2002; 3: 294-295. https://goo.gl/7AvX2f
7. Bhangle JR, Sathiya Narayanan VK, Deshpande SA. Dose linearity and uniformity of Siemens ONCOR impression plus linear accelerator designed for step-and-shoot intensity-modulated radiation therapy. J Med Phys. 2007; 32: 103-107. https://goo.gl/mdNpsp
8. Papanikolaou N, Mackie TR, Meger-Wells C, Gehring M, Reckwerdt P. Investigation of the convolution method for polyenergetic spectra. Med. Phys. 1993; 20: 1327-1336. https://goo.gl/2e8Jh4
9. Battles Z, Trefethen LN. An extension of Matlab to continuous functions and operators. SIAM J. Sci. Comput. 2006; 25: 1743-54. https://goo.gl/LC5TBt
10. Bray F, Jemal A, Grey N, Ferlay J, Forman D. Global cancer transitions according to the Human Development Index (2008-2030): a population-based study. Lancet Oncol. 2012; 13: 790-801. https://goo.gl/pkrHXK
11.  Sudhakar A. History of cancer, ancient and modern treatment methods. J Cancer Sci Ther. 2009; 1: 1-4. https://goo.gl/Y338rX
12. Ma CM. T, Pawlicki S, Jiang B, Li JS, Deng J, Mok E, et al. Monte Carlo verification of IMRT dose distributions from a commercial treatment planning optimization system. Phys. Med. Biol. 2000; 45: 2483-2495. https://goo.gl/PBY8t3
13. Jeraj R, Keall PJ, Siebers J.V. The effect of dose calculation accuracy on inverse treatment planning. Phys. Med. Biol. 2002; 47: 391-407. https://goo.gl/LD4xq5
14. Malicki J. The importance of accurate treatment planning, delivery, and dose verification. Rep Pract Oncol Radiother. 2012; 17: 63-65. https://goo.gl/n4hzFC  
15. Venselaar J, Welleweerd H, Mijnheer B. Tolerances for the accuracy of photon beam dose calculations of treatment planning systems. Radiother. Oncol. 2001; 60: 191-201. https://goo.gl/a9ncnV
16. Saarto T, Janes R, Tenhunen M, Kouri M. Palliative radiotherapy in the treatment of skeletal metastasis. Eur. J. Pain. 2002; 6: 323-330. https://goo.gl/AjfeAV