It is too costly and impractical to complete sleep measurements for all ages and combinations of sleep amounts and sleep debt. The possibility exists that mathematical equations can be developed and calibrated to simulate the various components of the sleep system. As a start for this development, equations were developed to predict the accumulation of each of the four sleep components (stage 1, stage 2, slow wave [stages 3 and 4] and REM) during sleep. Calibration was achieved using a published data set for people 30 years of age with partial sleep debt. Regression results were as follows: stage 1 (R² = 0.60, not significant), stage 2 (R² = 0.99, p < 0.001), slow wave (R² = 0.95, p < 0.01), REM (R² = 0.99, p < 0.001). All equations are continuous, smooth, and have stable boundary conditions. Future work is needed to adjust the calibration for various ages and non-debt conditions.

Introduction

Sleep is required for human life. Both short- and long-term consequences can develop when sleep is restricted or altered by sleep disorders. Sleep affects safety, mood, performance, and health [1].

In 1952, Rapid Eye Movement (REM) was discovered in relationship to sleep. This discovery was first observed and verified with human infants. As technology was applied to measure brainwaves during sleep, it was discovered that sleep varies or cycles (has architecture). Sleep pattern was first divided into REM and non-REM [2]. Later with more research, sleep architecture was defined further by subdividing non-REM sleep into stages 1, 2, 3, and 4 [2-6].

Sleep architecture has three major components (based on sleep time) defined by brainwave frequency and amplitude. These components are stage 2, slow wave (delta waves, stages 3 and 4), and REM. A fourth component, stage 1, provides a transition from awake to stage 2 and usually accounts for only a small portion of total sleep time. Stage 2 typically precedes slow wave and REM and seems to act like a switch or transition between slow wave and REM. Slow wave is a deep sleep (most difficult to wake an individual from sleep) that associates with exercise, fitness, and renewing of body components. REM sleep or paradoxical sleep produces a paralyzed body more or less but mentally active brain with dreams and low-amplitude, high-frequency brain waves similar to when a person is awake. Memory is consolidated during REM sleep. Most dreaming occurs during REM sleep.

Sleep components change as sleep progresses. These changes are clearly illustrated in sleep histograms. Sleep generally begins with stage 1 (usually a brief transition from awake to sleep). Stage 2 occurs next followed by slow wave (first stage 3 then stage 4) with a return to stage 2 followed by REM sleep. The pattern of stage 2, slow-wave, and REM sleep is repeated four or more times for adults achieving a full period of sleep. The first cycle typically has a relatively long period of slow-wave sleep, especially for active young people, after aerobic exercise, or after a period of total sleep loss. REM and stage 2 are relatively short during the first cycle. Slow wave more or less decreases exponentially from the first to last cycle. REM and stage 2 increases at a decreasing rate from the first to last cycle leveling off after two or three cycles. These general relationships have nonlinear effects on the build up of sleep debt for partial sleep loss. REM and stage 2 are cheated more than slow-wave sleep during partial sleep loss. Extended periods of sleep with increased cycles of sleep recover more REM and stage 2 than slow-wave sleep.

Superimposed on these relatively short-term dynamics, there are long-term, age-related changes in sleep components and amount of sleep. Neonates generally sleep 14 to 16 hours and have about 50 percent REM sleep at birth [7]. Cycle length is 50 to 60 minutes [6]. The REM percentage is even higher for preterm births [7]. The boundary condition at conception or shortly after conception appears to be near 100 percent REM [7]. At late teen or young adulthood, sleep amount drops to about eight hours with about 20 to 25 percent REM sleep [7,8]. Cycle length for adults is about 90 minutes but may be as high as 120 minutes [2,6]. In adults of 70 to 80 years of age, sleep amount is typically around six hours with REM sleep about 15 to 20 percent [7,8]. Slow-wave sleep approaches zero for inactive older adults [8].

In 2004, a special issue [9] of Aviation, Space, and Environmental Medicine was published to describe and review sleep models. In the preface Captain David Neri, Medical Service Corps, U. S. Navy [10], overviewed the need for mathematical models of sleep:

For many in the operational community, bio mathematical models of fatigue, sleepiness, and performance have become a significant issue. Military leaders, government policy makers, and commercial customers are looking for concrete answers to questions such as: how long can one work, fly, or drive without rest or sleep; how much sleep is required for recovery; what is the minimum sleep necessary to sustain performance; when is a person most at risk for an error, incident, or accident; and what countermeasures can be taken at what time(s) to reduce these risks to an acceptable level?

He reported in 2004 that mathematical models of sleep were only about 20 years old and that a need existed for better mathematical models of sleep. With the exception of one model [11], all the reported sleep models poorly predicted performance associated with partial sleep loss, while performing well in predicting performance for total sleep loss. The one model that predicted performance well for both total and partial sleep loss [11] did not include all sleep components. As medical technology develops relating health risks to sleep components or loss of sleep components, it is important to expand sleep models to include the details of sleep architecture.

The development of a complete system of equations to function as a sleep simulation model is lengthy. The development is beyond the scope of a single paper. The foundation for a more complete sleep model starts with mathematical descriptions of the sleep components during a night of sleep. The objective of this present work is to develop mathematical equations to describe the change in sleep for each component as a function of cycles completed. The equations are to be continuous, smooth, and stable from zero to the final number of cycles.

Model Development

Sleep architecture expressed in sleep histograms [2-6] display duration of sleep components for each cycle as sleep progresses. A change in duration of each component as cycle number increases is the bases for the starting point in the development of each component equation.

Slow-Wave Sleep

The amount of slow-wave sleep per cycle decreases approximately exponentially as the number of sleep cycles increase:

$D=d_1{e}^{-d_{2}N}$ (1)

Where D = slow-wave (delta wave) sleep per cycle

d₁ = constant

d₂ = decay rate

N = cycle number

This relationship derives from the following differential equation:

$\frac{dD}{dN}=-d_{2}D$ (2)

In other words the rate of change in slow-wave sleep per cycle is proportional to the slow-wave sleep per cycle. To get total slow-wave sleep for a sleep period, Equation 1 must be integrated over the number of sleep cycles used:

$D_T=d_1{\displaystyle \underset{0}{\overset{N_T}{\int }}{e}^{-d_{{}_2}^{}N}}$ (3)

Where D_T = total slow-wave sleep through end of current cycle

N_T = number of cycles completed

Steps of the integration process are given in Appendix I. Completion of this integration yields

$D_T=\frac{d_1}{d_2}\left(1-e^{-d_2{N}_T}\right)$ (4)

Note that nothing is inferred about stage 1 (transition to sleep), stage 2, REM, or WASO (time awake after sleep onset) that also may occur during a cycle. Equation 4 only predicts the increase in slow-wave sleep as sleep cycles increase.

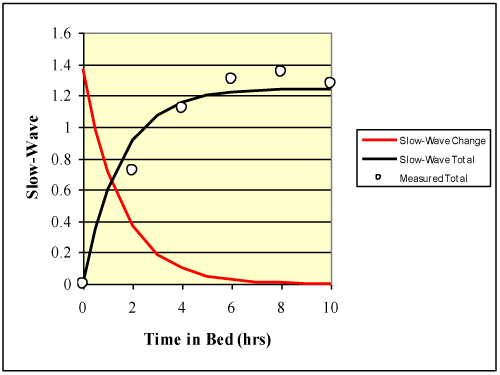
Predictions from Equation 4 were compared to measured data from Banks et al. [12]. The measured data provided by Banks et al. [12] were for a mixture of men and women with an average age of 30.4 years. Results are shown in (Figure 1). The number of sleep cycles was not reported. A 90-minute sleep cycle [2,6] was assumed. A total sleep time of about nine hours was reported leading to six cycles of sleep. Time in bed was converted to sleep cycles to produce the results shown in (Figure 1) An R² = 0.95 was obtained, which was significant (p < 0.01) using Student t distribution to compute the probability of type I error. Values for d₁ and d₂ are 1.37 and 1.1 respectively. These data were collected after five nights of sleep restricted to four hours in bed. Because these results are for recovery from sleep debt, these calibration values may differ from a normal night of sleep. Equation 4 seems to be sufficient to describe the non-linear changes in slow-wave sleep as sleep cycles increase. The data and the model both level off after about six hours (four cycles).

REM Sleep

The amount of REM sleep per cycle starts low and increases approximately as a saturating exponential as cycles increase:

$R=r_1(1-e^{-r_{2}N})$ (5)

Where R = REM sleep per cycle

r₁ = constant

r² = decay coefficient

To get total REM sleep, the right side of Equation 5 must be integrated from zero through the total number of cycles:

$R_T=r_1{\displaystyle \underset{0}{\overset{N_T}{\int }}\left(1-e^{-r_{2}N}\right)}$ (6)

Figure 1: Comparison of predicted and measured slow-wave sleep after five days of restricted sleep. Data from Banks et al. [12].

The details of integration are presented in Appendix II. The resulting equation is

$R_T=r_1\left(N_T-\frac{1}{r_2}(1-e^{-r_2{N}_T})\right)$ (7)

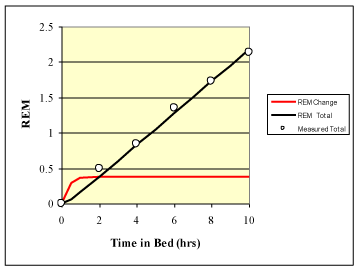
Banks et al. [12] also measured the recovery of REM sleep in association with time in bed. Time in bed was converted to sleep cycles as discussed with slow-wave sleep. An R² = 0.99 was obtained comparing predictions with Equation 7 to measured results. The results were highly significant (p < 0.001). Values for r₁ and R² were 0.375 and 5.0 respectively. Results for REM sleep are shown in (Figure 2).

Figure 2: Comparison of measured and predicted REM sleep as a function of time in bed during recovery from five days of sleep restriction. Data from Banks et al. [12].

Stage 2 Sleep

Stage 2 sleep appears linear with increase in cycle number after the first or second cycle in sleep histograms. Stage 2 in the first sleep cycle is usually less than the amount in later sleep cycles. A saturating exponential function will produce this trend as cycle number increases:

$S{2}_T=s_1{\displaystyle \underset{0}{\overset{N_T}{\int }}\left(1-e^{-s_{2}N}\right)}$ (8)

Equation 8 must be integrated to obtain the total amount of stage 2 sleep. Integration steps are provided in Appendix III. The following equation was obtained:

$S{2}_T=s_1\left(N_T-\frac{1}{s_2}(1-e^{-s_2{N}_T})\right)$ (9)

Where s₂T = total stage 2 Sleep

s₁ = constant

s₂ = decay coefficient

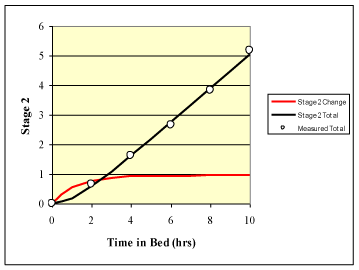
Banks et al. [12] also measured data for stage 2. A comparison of measured and predicted s₂T values yielded an R² = 0.99. The results were highly significant (p < 0.001). Values for s₁ and s₂ were 0.95 and 1.4 respectively. Figure 3 illustrates the measured data and predictions from Equation 9.

Figure 3: Comparison of measured and predicted stage 2 sleep. Data from Banks et al. [12].

Stage 1 Sleep

Stage 1 sleep is usually small in magnitude in comparison to other sleep components. For individuals, it occurs more or less randomly throughout an evening of sleep. It does not seem to have much of a pattern. Most sleep histograms for a typical night of sleep present a constant distribution. An increase of stage 1 sleep above typical values is an important indicator of obstructive sleep apnea.

The amount of stage 1 sleep per cycle was assumed to be constant but highly variable. The integration of a constant over a night of sleep produces a linear equation with intercept of zero (correct boundary condition at the beginning of sleep:

$S{1}_T=s{1}_1{N}_T$ (10)

Where s₁T = total stage 1 Sleep

s₁1 = constant

In the study by Banks et al. [12], stage 1 was not reported. Because the other sleep components and total sleep were published, it was possible to estimate values for stage 1 by subtracting the sum of the reported components from total sleep reported. The accuracy, however, was limited by the ability to digitize data from the published graphs of slow wave, REM, stage 2, and total sleep amount. Measured values were compared to predicted values from Equation 10 with s₁1 = to 0.065. This linear equation explained 60 percent (R² = 0.60) of the variability of stage 1 but was not significant. The measured values for cycles 5 and 6 (time in bed = 8 and 10 hours) in the Banks et al. study [12] were 0.39 and 0.32. The predicted values for cycles 5 and 6 were 0.35 and 0.43. A comparable stage 1 measured value of 0.44 for age 30 was obtained from an independent study [8]. Stage 1 sleep ranges from 2 to 16 percent of total sleep in this independent study. Considering the high variability of stage 1 sleep, Equation 10 as calibrated is a reasonable estimate for stage 1 sleep. As mentioned earlier, stage 1 sleep associates with obstructive sleep apnea. It is expected that the calibration value of 0.065 increases as severity of obstructive sleep apnea increases.

Discussion

With the exception of stage 1, predictions from all component equations were significant or highly significant with R² values above 0.95. The data set from Banks et al. [12] is unique in that it contains measurements of components for a range of time in bed values. Measured results are averages from 21 to 29 individuals within each recovery sleep dose. It seems to be one of the superior data sets for varying sleep amounts. It was designed to evaluate recovery after partial sleep loss. The calibration coefficients for all components are specific to recovery from a sleep dept condition.

The idea for the initial distribution of each sleep component, however, was obtained from several published sleep histograms for a normal night of adult sleep. The integrated and final equation to predict each component was, thus, obtained from non-debt sleep conditions. It appears that the form of each final equation is valid for both normal and sleep debt conditions. The calibration coefficients need to be evaluated for non-debt conditions. The calibration is also restricted to adults of about 30 years of age.

Cycle number for a normal night of sleep decreases with age. At birth, total sleep of 14 to 16 hours [7] with a cycle length of 50 minutes [6] results in 17 to 19 cycles. An adult that spends 8 hours of time in bed with a 90-minute sleep cycle will experience 5.3 cycles. There is a need to develop a function to determine the number of sleep cycles as a function of age. Once a function for sleep cycles with age is developed, there is a need to evaluate the coefficients for each component equation as a function of age and for normal and sleep debt conditions.

At present time, there is not a complete data set from birth to senior ages for all components with varying times in bed to test a complete model. To obtain such a data set would be costly. The study by Banks et al. [12] included 159 healthy adults aged 22 to 45 (mean 30.4, standard deviation 7.0) with 49.1 percent female. If a similar study were performed for neonates, infants, one, two, five, seven, 10, 15, 20, 25, 30, 40, 50 60, 70, and 80 years of age to fully define changes with age, 2544 people would need to be evaluated just for normal sleep. If two levels of sleep debt were also evaluated from age 10 through 80 years, another 3180 people would be added to the study. The time and cost to evaluate sleep for 5000 plus people seems prohibitive. It has not been done. Sleep surveys are cheaper but do not measure sleep components.

The possible sleep study proposed above may be larger than needed, especially after an initial component model has been completed. It may be possible to reduce the number of adult ages considered because total sleep changes from ages 30 to 80 are small and appear to linearly decrease with age [8]. WASO (not modeled in this paper) increases at an increasing rate during this age range [8]. There is evidence that aerobic exercise can have a significant effect on the reduction of WASO [13,14]. There is also evidence that aerobic exercise increases slow-wave sleep [15-17]. How much can WASO be reduced by exercise is an important question that needs to be addressed by measured data and modeling. Exercise or aerobic fitness adds another variable that needs to be included in the mathematical model and adds a need for more data collection. Components of REM, slow-wave, and WASO (low sleep efficiency) have all been associated with sleep disorders.

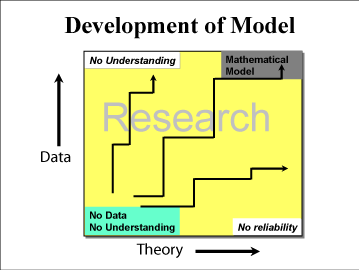
The objective of research is not just to collect data or just develop a model. The objective is to gain understanding. The advantage to consider data needs and model development together is illustrated in (Figure 4). Data alone may not provide understanding. Ideas or theory does not provide reliability. Some understanding can help focus data collection and some data can help focus the development of better ideas and understanding.

Figure 4: Illustration of data and theory working together to gain reliable understanding or mathematical model.

A much reduced data set similar to that of Banks et al. [12] for children after the need of naps (maybe age seven) and for seniors coupled with the existing data of Banks et al. [12] would be an important contribution to test the existing component equations developed in this paper. Number of cycles used for sleep needs to be measured. With these additional data sets, both data collection and model development could then be re-evaluated for future work.

Cost to collect data can also be greatly reduced by reducing the number of people in each time restriction to seven instead of the 21 to 29 used [12]. In model development and testing, a reliable mean at each setting is the objective. The goal is not to achieve a significant difference between each setting. There is no need to approach 30 in the sample size at each setting to obtain a normal distribution of the errors about the mean. Furthermore, the data at other setting can often be used to detect and eliminate outliers. With seven as a sample size at each setting, one individual contributes slightly less than 15 percent to the mean value.

Also, it may be possible to piece together the current data sets with reasonable assumptions to substitute for missing data to build an acceptable but questionable model from birth to senior ages. This model could then be used to determine data needed to verify, reject or modify the model. It is recommended that such a model be attempted in the future, building on the component equations presented within this paper.

To do nothing forces people to make judgments based on the limited data available. Nobel Prize winner, Lord Kelvin’s advice seems to apply [18]

I often say that when you can measure what you are speaking about, and express it in numbers, you know something about it; but when you cannot express it in numbers, your knowledge is of a meager and unsatisfactory kind; it may be the beginning of knowledge, but you have scarcely, in your thoughts, advanced to the stage of Science, whatever the matter may be.

1. Gregory J.  Sleep: A Good Investment in Health and Safety.  J. Agromedicine 2008; 13: 119-131. https://goo.gl/BKRnyr
2. Walker M.  Why We Sleep: Unlocking the Power of Sleep and Dreams.  Scribner, New York.  2017. https://goo.gl/zpKVRj
3. Coleman R.M.  Wide Awake at 3:00 A.M. by Choice or by Chance?  W. H. Freeman and Company, New York, 1986. https://goo.gl/QaQEC4
4. Hauri P, Linde S.  No More Sleepless Nights.  John Wiley and Sons, Inc., Hoboken, New Jersey. 1996. https://goo.gl/utvV81
5. Maas J, Wherry M, Axelrod D, Hogan B, Blumin J.  Power Sleep:The Revolutionary Program that Prepares Your Mind for Peak Performance.  HarperPerennial , New York. 1998. https://goo.gl/8G2wTR   
6. Carskadon M, Dement W.  Normal Human Sleep: An Overview, Chapter 2. in Kryger M H, T Roth, W C Dement, Editors, Principles and Practice of Sleep Medicine, 4th Ed. Elsevier Saunders, Philadelphia, Pennsylvania.  2005. https://goo.gl/9ejtJc
7. Roffwarg HP, Muzio JN, Dement W.  Ontogenetic Development of the Human Sleep-Dream Cycle.  Science. 1966; 152: 604-619. https://goo.gl/Cm3V5C
8. Ohayon M, Carskadon M, Guilleminault C, Vitiello M.  Metaanalysis of Quantitative Sleep Parameters from Childhood to Old Age in Healthy Individuals: Developing Normative Sleep Values across the Human Lifespan.  SLEEP 2004; 27: 1255-1273. https://goo.gl/dKRy3c
9. Neri D. (Supplement Editor).  Proceedings of the Fatigue and Performance Modeling Workshop June 13-14, 2002, Seattle, WA.  Aviation, Space, and Environmental Medicine 2004; 75.
10. Neri DF.  Preface: Fatigue and Performance Modeling Workshop, June 13-14, 2002. Aviat Space Environ Med.  2004; 75: 1-3. https://goo.gl/WYpaJc
11. Gregory J, Xie X, Mengel S.  SLEEP (Sleep Loss Effects on Everyday Performance) Model.  Aviation, Space, and Environmental Medicine. 2004; 75: 125-133. https://goo.gl/21CZ54
12. Banks S, Dongen HP, Maislin G, Dinges DF. Neurobehavioral Dynamics Following Chronic Sleep Restriction: Dose-Response Effects of One Night for Recovery.  Sleep 2010; 33: 1013-1026. https://goo.gl/QUQk49
13. Passos G, Poyares D, Santana M, D’Aurea C, YoungsteD_T S, Tufik S, et al.  Effects of Moderate Aerobic Exercise Training on Chronic Primary Insomnia.  Sleep Medicine. 2011; 12: 1018-1027. https://goo.gl/6Z8eHf
14. Doleza B, Neufeld E, Boland D, Martin J, Cooper C.  Interrelationship between Sleep and Exercise: A Systematic Review.  Advances in Preventive Medicine. 2017. https://goo.gl/gF2AGd
15. Shapiro CM, Bortz R, Mitchell D, Bartel P, Jooste P.  Slow-Wave Sleep: a Recovery Period after Exercise.  Science. 1981; 214: 1253-1254. https://goo.gl/quVmCL
16. Bunnell D, Bevier W, Horvath S.  Effects of Exhaustive Exercise on the Sleep of men and Women.  Psychophysiology 2007; 20: 50-58. https://goo.gl/kyZXwK
17. Baekeland F, Lasky R.  Exercise and Sleep Patterns in College Athletes.  Perceptual and Motor Skills. 1966; 23: 1203-1207. https://goo.gl/s5WrCZ
18. Sears F, Zemansky M.  University Physics 3rd Ed.  Addison-Wesley Publishing Company, Inc, Reading, Massachusetts. 1964.